Work in progress
Effect of gaussian noise and/or dropout during training phase on model’s performance.
DONE:
noise implementation
dropout implementation
main testing loop
improve histogram visualisation (equal bins, opacity)
TODO:
check if dropout causes more neurons to spike
noise robustness vs depth
Imports¶
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors
import matplotlib.cm
import torch
import torch.nn as nn
from tqdm.auto import tqdm as pbar
dtype = torch.float
if torch.cuda.is_available():
device = torch.device("cuda")
torch.cuda.empty_cache()
else:
device = torch.device("cpu")Hyperparameters¶
# Constants
SECONDS = 1
MS = 1e-3
HZ = 1
DT = 1 * MS # large time step to make simulations run faster
ANF_PER_EAR = 100 # repeats of each ear with independent noise
DURATION = .1 * SECONDS # stimulus duration
DURATION_STEPS = int(np.round(DURATION / DT))
INPUT_SIZE = 2 * ANF_PER_EAR
mu, sigma = 0, 0.5 # gaussian noise for phase delay
# Training
LR = 0.005
N_EPOCHS = 20
batch_size = 64
n_training_batches = 64
n_testing_batches = 32
num_samples = batch_size*n_training_batches
dropout_prob = 0.5
RUNS = 3
# classes at 15 degree increments
NUM_CLASSES = 180 // 15
print(f'Number of classes = {NUM_CLASSES}')
# Network
NUM_HIDDEN = 30 # number of hidden units
TAU = 5 # membrane time constant
IE_RATIO = 0.5 # ratio of inhibitory:excitatory units (used if DALES_LAW = True). 0 = all excitatory, 1 = all inhibitory
DALES_LAW = False # When True, units will be only excitatory or inhibitory. When False, units will use both (like a normal ANN)
if DALES_LAW:
print('Using Dales Law')Number of classes = 12
Functions¶
Stimulus¶
def input_signal(ipd, sigma=sigma, mu=mu):
"""
Generate an input signal (spike array) from array of true IPDs
"""
envelope_power = 2 # higher values make sharper envelopes, easier
rate_max = 600 * HZ # maximum Poisson firing rate
stimulus_frequency = 20 * HZ
num_samples = len(ipd)
times = np.arange(DURATION_STEPS) * DT # array of times
phi = 2*np.pi*(stimulus_frequency * times + np.random.rand()) # array of phases corresponding to those times with random offset
# each point in the array will have a different phase based on which ear it is
# and its delay
theta = np.zeros((num_samples, DURATION_STEPS, 2*ANF_PER_EAR))
# for each ear, we have ANF_PER_EAR different phase delays from to pi/2 so
# that the differences between the two ears can cover the full range from -pi/2 to pi/2
phase_delays = np.linspace(0, np.pi/2, ANF_PER_EAR)
# add gaussian noise to phase delays
phase_noise = np.random.normal(mu, sigma, 2*ANF_PER_EAR)
noisy_delays_l = phase_delays + phase_noise[:ANF_PER_EAR]
noisy_delays_r = phase_delays + phase_noise[ANF_PER_EAR:]
# now we set up these theta to implement that. Some numpy vectorisation logic here which looks a little weird,
# but implements the idea in the text above.
theta[:, :, :ANF_PER_EAR] = phi[np.newaxis, :, np.newaxis]+noisy_delays_l[np.newaxis, np.newaxis, :]
theta[:, :, ANF_PER_EAR:] = phi[np.newaxis, :, np.newaxis]+noisy_delays_r[np.newaxis, np.newaxis, :]+ipd[:, np.newaxis, np.newaxis]
# now generate Poisson spikes at the given firing rate as in the previous notebook
spikes = np.random.rand(num_samples, DURATION_STEPS, 2*ANF_PER_EAR)<rate_max*DT*(0.5*(1+np.sin(theta)))**envelope_power
return spikes
def random_ipd_input_signal(num_samples, tensor=True, sigma=sigma):
"""
Generate the training data
Returns true IPDs from U(-pi/2, pi/2) and corresponding spike arrays
"""
ipd = np.random.rand(num_samples)*np.pi-np.pi/2 # uniformly random in (-pi/2, pi/2)
spikes = spikes_from_fixed_idp_input_signal(ipd, tensor, sigma=sigma)
if tensor:
ipd = torch.tensor(ipd, device=device, dtype=dtype)
return ipd, spikes
def spikes_from_fixed_idp_input_signal(ipd, tensor=True, sigma=sigma):
spikes = input_signal(ipd, sigma=sigma)
if tensor:
spikes = torch.tensor(spikes, device=device, dtype=dtype)
return spikes
def show_examples(shown=8):
ipd = np.linspace(-np.pi/2, np.pi/2, shown)
spikes = spikes_from_fixed_idp_input_signal(ipd, shown).cpu()
plt.figure(figsize=(10, 4), dpi=100)
for i in range(shown):
plt.subplot(2, shown // 2, i+1)
plt.imshow(spikes[i, :, :].T, aspect='auto', interpolation='nearest', cmap=plt.cm.gray_r)
plt.title(f'True IPD = {int(ipd[i]*180/np.pi)} deg')
if i>=4:
plt.xlabel('Time (steps)')
if i%4==0:
plt.ylabel('Input neuron index')
plt.tight_layout()
def data_generator(ipds, spikes):
perm = torch.randperm(spikes.shape[0])
spikes = spikes[perm, :, :]
ipds = ipds[perm]
n, _, _ = spikes.shape
n_batch = n//batch_size
for i in range(n_batch):
x_local = spikes[i*batch_size:(i+1)*batch_size, :, :]
y_local = ipds[i*batch_size:(i+1)*batch_size]
yield x_local, y_local
def discretise(ipds):
return ((ipds+np.pi/2) * NUM_CLASSES / np.pi).long() # assumes input is tensor
def continuise(ipd_indices): # convert indices back to IPD midpoints
return ((ipd_indices+0.5) / NUM_CLASSES * np.pi - np.pi / 2) #* (NUM_CLASSES+1) / NUM_CLASSESSNN¶
def sigmoid(x, beta):
return 1 / (1 + torch.exp(-beta*x))
def sigmoid_deriv(x, beta):
s = sigmoid(x, beta)
return beta * s * (1 - s)
class SurrGradSpike(torch.autograd.Function):
@staticmethod
def forward(ctx, inp):
ctx.save_for_backward(inp)
out = torch.zeros_like(inp)
out[inp > 0] = 1.0
return out
@staticmethod
def backward(ctx, grad_output):
inp, = ctx.saved_tensors
sigmoid_derivative = sigmoid_deriv(inp, beta=5)
grad = grad_output*sigmoid_derivative
return grad
spike_fn = SurrGradSpike.apply
def membrane_only(input_spikes, weights, tau):
"""
:param input_spikes: has shape (batch_size, duration_steps, input_size)
:param weights: has shape (input_size, num_classes
:param tau:
:return:
"""
batch_size = input_spikes.shape[0]
assert len(input_spikes.shape) == 3
v = torch.zeros((batch_size, NUM_CLASSES), device=device, dtype=dtype)
v_rec = [v]
h = torch.einsum("abc,cd->abd", (input_spikes, weights))
alpha = np.exp(-DT / tau)
for t in range(DURATION_STEPS - 1):
v = alpha*v + h[:, t, :]
v_rec.append(v)
v_rec = torch.stack(v_rec, dim=1) # (batch_size, duration_steps, num_classes)
return v_rec
def layer1(input_spikes, w1, tau, sign1):
if DALES_LAW:
w1 = get_signed_weights(w1, sign1)
batch_size = input_spikes.shape[0]
# First layer: input to hidden
v = torch.zeros((batch_size, NUM_HIDDEN), device=device, dtype=dtype)
s = torch.zeros((batch_size, NUM_HIDDEN), device=device, dtype=dtype)
s_rec = [s]
h = torch.einsum("abc,cd->abd", (input_spikes, w1))
alpha = np.exp(-DT / tau)
for t in range(DURATION_STEPS - 1):
new_v = (alpha*v + h[:, t, :])*(1-s) # multiply by 0 after a spike
s = spike_fn(v-1) # threshold of 1
v = new_v
s_rec.append(s)
s_rec = torch.stack(s_rec, dim=1)
return s_rec
def layer2(s_rec, w2, tau, sign2):
"""Second layer: hidden to output"""
if DALES_LAW:
w2 = get_signed_weights(w2, sign2)
v_rec = membrane_only(s_rec, w2, tau=tau)
return v_rec
def dropout_layer(input, p=dropout_prob):
dropout = torch.nn.Dropout(p=p)
output = dropout(input)
return output
def snn(input_spikes, w1, w2, signs, tau=5*MS, inference=False, p=0):
"""Run the simulation"""
#dropout = torch.nn.Dropout(p=0.9)
s_rec = layer1(input_spikes, w1, tau, signs[0])
if not inference:
s_rec = dropout_layer(s_rec, p=p)
v_rec = layer2(s_rec, w2, tau, signs[1])
# Return recorded membrane potential of output
return v_recDale’s Law¶
def get_dales_mask(nb_inputs, nb_out, ie_ratio) :
d_mask = torch.ones(nb_inputs, nb_out)
#inhib_units = np.random.choice(nb_inputs, int(nb_inputs*ie_ratio), replace=False)
inhib_units = torch.arange(ie_ratio*nb_inputs, dtype=int)
d_mask[inhib_units, :] = -1
return d_mask
def init_weight_matrices(ie_ratio = 0.1):
"""Weights and uniform weight initialisation"""
# Input to hidden layer
w1 = nn.Parameter(torch.empty((INPUT_SIZE, NUM_HIDDEN), device=device, dtype=dtype, requires_grad=True))
fan_in, _ = nn.init._calculate_fan_in_and_fan_out(w1)
bound = 1 / np.sqrt(fan_in)
nn.init.uniform_(w1, -bound, bound)
# Hidden layer to output
w2 = nn.Parameter(torch.empty((NUM_HIDDEN, NUM_CLASSES), device=device, dtype=dtype, requires_grad=True))
fan_in, _ = nn.init._calculate_fan_in_and_fan_out(w2)
bound = 1 / np.sqrt(fan_in)
nn.init.uniform_(w2, -bound, bound)
#Get fixed signs for the weight, 90% excitatory
signs = [get_dales_mask(*w.shape, ie_ratio).to(w.device) for w in (w1, w2)]
return w1, w2, signs
def get_signed_weights(w, sign):
"""Get the signed value of the weight"""
# Note abs is in principle not differentiable.
# In practice, pytorch will set the derivative to 0 when the values are 0.
# (see https://discuss.pytorch.org/t/how-does-autograd-deal-with-non-differentiable-opponents-such-as-abs-and-max/34538)
# This has the adverse effect that, during training, if a synapse reaches 0,
# it is "culled" and can not be recovered.
# It should be possible to cheat here and either "wiggle" 0-valued synapses,
# or to override abs gradient to return a very small random number.
#TODO try ReLu or other activation
#TODO reproduce paper https://www.biorxiv.org/content/10.1101/2020.11.02.364968v2.full
# return torch.max(w, 0)*sign
return torch.abs(w)*signTraining¶
def train(w1, w2, signs, ipds, spikes, ipds_validation, spikes_validation, lr=0.01, n_epochs=30, tau=5*MS, p=0, viz=False):
"""
:param lr: learning rate
:return:
"""
# Optimiser and loss function
optimizer = torch.optim.Adam([w1, w2], lr=lr)
log_softmax_fn = nn.LogSoftmax(dim=1)
loss_fn = nn.NLLLoss()
loss_hist = []
val_loss_hist = []
best_loss = 1e10
val_loss_best_loss = 1e10
for e in range(n_epochs):
local_loss = []
for x_local, y_local in data_generator(discretise(ipds), spikes):
# Run network
output = snn(x_local, w1, w2, signs, tau=tau, inference=False, p=p)
# Compute cross entropy loss
m = torch.sum(output, 1)*0.01 # Sum time dimension
reg = 0
loss = loss_fn(log_softmax_fn(m), y_local) + reg
local_loss.append(loss.item())
# Update gradients
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_hist.append(np.mean(local_loss))
val_local_loss = []
for x_local, y_local in data_generator(discretise(ipds_validation), spikes_validation):
# Run network
output = snn(x_local, w1, w2, signs, tau=tau)
# Compute cross entropy loss
m = torch.sum(output, 1)*0.01 # Sum time dimension
val_loss = loss_fn(log_softmax_fn(m), y_local)
val_local_loss.append(val_loss.item())
val_loss_hist.append(np.mean(val_local_loss))
if np.mean(val_local_loss) < val_loss_best_loss:
val_loss_best_loss = np.mean(val_local_loss)
if DALES_LAW:
best_weights = get_signed_weights(w1, signs[0]), get_signed_weights(w2, signs[1]), signs
else:
best_weights = w1, w2, signs
#Early Stopping :
if torch.tensor(val_loss_hist[-10:]).argmin() == 0 and e>10:
print('Early Stop !')
break
# Plot the loss function over time
if viz:
plt.plot(loss_hist)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.tight_layout()
plt.plot(val_loss_hist)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.tight_layout()
if DALES_LAW:
return get_signed_weights(w1, signs[0]), get_signed_weights(w2, signs[1]), signs
else:
return w1, w2, signsTesting¶
def test_accuracy(ipds, spikes, run):
accs = []
ipd_true = []
ipd_est = []
confusion = np.zeros((NUM_CLASSES, NUM_CLASSES))
for x_local, y_local in data_generator(ipds, spikes):
y_local_orig = y_local
y_local = discretise(y_local)
output = run(x_local)
m = torch.sum(output, 1) # Sum time dimension
_, am = torch.max(m, 1) # argmax over output units
tmp = np.mean((y_local == am).detach().cpu().numpy()) # compare to labels
for i, j in zip(y_local.detach().cpu().numpy(), am.detach().cpu().numpy()):
confusion[j, i] += 1
ipd_true.append(y_local_orig.cpu().data.numpy())
ipd_est.append(continuise(am.detach().cpu().numpy()))
accs.append(tmp)
ipd_true = np.hstack(ipd_true)
ipd_est = np.hstack(ipd_est)
return ipd_true, ipd_est, confusion, accs
def report_accuracy(ipd_true, ipd_est, confusion, accs, label, verbose = False, viz = False):
abs_errors_deg = abs(ipd_true-ipd_est)*180/np.pi
if verbose:
print()
print(f"{label} classifier accuracy: {100*np.mean(accs):.1f}%")
print(f"{label} absolute error: {np.mean(abs_errors_deg):.1f} deg")
if viz:
plt.figure(figsize=(10, 4), dpi=100)
plt.subplot(121)
plt.hist(ipd_true * 180 / np.pi, bins=NUM_CLASSES, range=[-90,90], alpha = 0.75, label='True')
plt.hist(ipd_est* 180 / np.pi, bins=NUM_CLASSES, range=[-90,90], alpha = 0.75, label='Estimated')
plt.xlabel("IPD")
plt.yticks([])
plt.legend(loc='best')
plt.title(label)
plt.subplot(122)
confusion /= np.sum(confusion, axis=0)[np.newaxis, :]
plt.imshow(confusion, interpolation='nearest', aspect='equal', origin='lower', extent=(-90, 90, -90, 90))
plt.xlabel('True IPD')
plt.ylabel('Estimated IPD')
plt.title('Confusion matrix')
plt.tight_layout()
def analyse_accuracy(ipds, spikes, run, label):
ipd_true, ipd_est, confusion, accs = test_accuracy(ipds, spikes, run)
report_accuracy(ipd_true, ipd_est, confusion, accs, label)
return 100*np.mean(accs), np.mean(abs(ipd_true-ipd_est)*180/np.pi)Train Network¶
Analysis¶
dropouts = [0, 0.5, 0.9]
sigmas = [0, 0.1, 0.2, 0.3, 0.4, 0.5]
plots = ['train_acc', 'train_err', 'test_acc', 'test_err']
all_runs_results = []
for run in pbar(range(RUNS), leave=False, desc="Runs"):
results = {key:{f'p_{dropout}':list() for dropout in dropouts} for key in plots}
for dropout_prob in pbar(dropouts, leave=False, desc="Dropouts"):
for sigma in pbar(sigmas, leave=False, desc="Sigmas"):
w1, w2, signs = init_weight_matrices(ie_ratio=IE_RATIO)
ipds_training, spikes_training = random_ipd_input_signal(num_samples, sigma=sigma)
ipds_validation, spikes_validation = random_ipd_input_signal(num_samples, sigma=sigma)
w1_trained, w2_trained, signs = train(w1, w2, signs, ipds_training, spikes_training, ipds_validation, spikes_validation, lr=LR, n_epochs=N_EPOCHS, tau=TAU*MS, p=dropout_prob)
run_func = lambda x: snn(x, w1_trained, w2_trained, signs, inference=True)
train_acc, train_err = analyse_accuracy(ipds_training, spikes_training, run_func, 'Train')
ipds_test, spikes_test = random_ipd_input_signal(batch_size*n_testing_batches, sigma=0)
test_acc, test_err = analyse_accuracy(ipds_test, spikes_test, run_func, 'Test')
for plot, metric in zip(plots, [train_acc, train_err, test_acc, test_err]):
results[plot][f'p_{dropout_prob}'].append(metric)
all_runs_results.append(results)
#Plot
from scipy.stats import sem
from statistics import mean, stdev
import math
r = {key:{f'p_{dropout}':list() for dropout in dropouts} for key in plots}
yerr = {key:{f'p_{dropout}':list() for dropout in dropouts} for key in plots}
plt.figure(figsize=(16, 4), dpi=100)
for i, plot in enumerate(plots):
temp = 141+i
plt.subplot(temp)
for p in dropouts:
r[plot][f'p_{p}'] = [mean(list(all_runs_results[x][plot][f'p_{p}'][s] for x in range(RUNS))) for s in range(len(sigmas))]
yerr[plot][f'p_{p}'] = [stdev(list(all_runs_results[x][plot][f'p_{p}'][s] for x in range(RUNS)))/math.sqrt(RUNS) for s in range(len(sigmas))]
plt.errorbar(sigmas, r[plot][f'p_{p}'], yerr=yerr[plot][f'p_{p}'], label=f'Dropout p={p}')
plt.xlabel("sigma")
plt.title(plot.title())
if i % 2 == 0:
plt.ylim([0, 100])
plt.ylabel('Accuracy (%)')
else:
plt.ylabel('Mean error (deg)')
plt.legend()
plt.tight_layout() 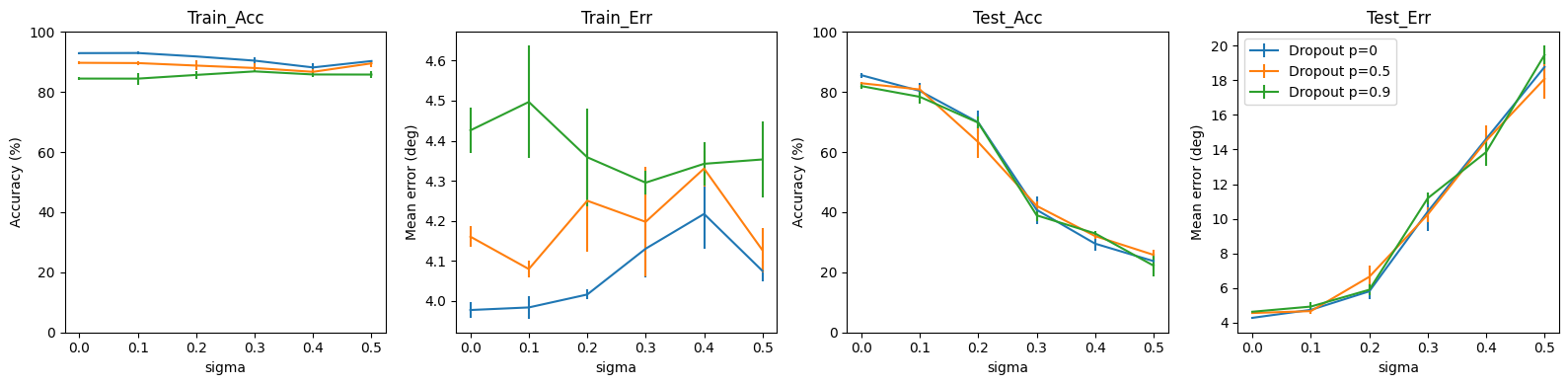
Conclusions¶
dropout doesn’t do much - difference between train/test performance is smaller, but final accuracy and error remain the same. Even very high values of p don’t affect training too much, probably because few neurons spike either way. Could be interesting to check if dropout activates more neurons (maybe targeted dropout affecting only the spiking neurons? though the network is probably too simple for it to be useful for this problem)
absolute test error starts to grow moreless linearly after certain threshold